Solver
From Sokoban Wiki
Terms and Definitions
- Level
- Another term for a Sokoban puzzle.
- A level contains a board and usually additional data like title, author name and solutions.
- Sometimes it’s also called “maze”.
- Board
- The board is a 2 dimensional area containing the objects of a Sokoban level (walls, boxes, goals, player and empty squares).
- Boxes
- The objects on the board which the player can push around.
- Goals
- The target positions for the boxes.
- A level is solved when all boxes have been pushed to a goal.
- Box Configuration
- The positions of all boxes on the board form a specific Box Configuration.
- Board position
- The positions of all boxes and the player position constitute a Board Position.
- State
- The positions of all boxes and the player position constitute a Board Position.
- The term State is used when additional data are stored together with a Board Position.
- For instance, a solver may store: pushes needed to reach the board position or the information of which box has been pushed last.
- The search tree consists of states being generated during the search.
- States can be stored in a transposition table so duplicate game positions can be detected, for instance.
- Other terms for a state are: game position, game state and game position.
- Player reachable area
- The player reachable area consists of all squares on the board currently reachable for the player.
- Corral
- The boxes and walls on the board can split the board into several areas.
- An area of the board which the player cannot reach, surrounded by a barrier made of one or more boxes, and any number of walls is called “corral”.
Data Structures
Positions on the board
The board is a two-dimensional area containing the objects of a Sokoban level.
Hence, a natural data structure for storing the board is a two-dimensional array.
However, many solvers use a one-dimensional data structure for this task, numbering the board positions from 0 to n-1, where 'n' is the number of board squares.
Accessing the elements of a one-dimensional vector is easier and faster for a computer program than accessing the elements of a two-dimensional array, simply because the address calculation is less complicated.
Using a one-dimensional vector has also the advantage for the programmer, that a square number can be stored in just one variable.
The board data structure can also include additional data, for instance flags for:
- Is a box frozen?
- Is the position a dead position?
Storing a state
In Sokoban a state consists (among possible additional data associated with it) of the positions of the boxes and the position of the player.
Every other element of the board cannot change its position and therefore needn’t to be stored per state.
Therefore a state can be stored by using:
- One integer array for storing all box positions.
- One integer for storing the player position.
For a better memory alignment the player position and box positions can also be stored in one integer array together.
The data structure usually consists of additional data fields like for storing information about the state like pushes needed to reach it or which box has been pushed last.
Example data structure for Java:
public class State {
int[] boxPositions;
int playerPosition;
}
Transposition Tables
Solvers for the Sokoban game use a graph search as the search algorithm.
The search creates a directed graph of states.
In nearly every Sokoban puzzle many states can be reached through different paths in the search graph.<br / In these cases the graph is cyclic and the search reaches specific states multiple times during the search.<br / The search effort can therefore be considerably reduced by eliminating duplicate states from the search.<br / A common technique is to use a large hash table, called the transposition table, which stores all already explored states.<br /
The transposition can also be used to store additional data per state – for instance the depth the state has been reached in during an IDA*-search.
Tradeoff between space and time
The transposition table may need to hold several million states.<br / Hence, an efficient data structure has to be chosen for storing the states.
There are different approaches to address the high memory usage problem.
Limit the transposition table size
One solution for the high memory usage of the transposition is limiting the size of the transposition table.
This makes the search algorithm a kind of hybrid between tree search and graph search. <br / The advantage is the ability to search for solutions for larger levels due to the lower memory usage, while an obvious disadvantage is that it may lead to duplicated search effort.
Incremental storage of states
Instead of storing all box positions and the (normalized) player position for every state it’s also possible to store the data relative to another state.
This divides the states in two types:
- States that store all box positions and the player position.
- States that store a link to another state and the difference to that linked state.
Example:<br / A state consists of these data:
State 1: box positions: 10, 13, 21, 33, 45, 47, 48, 49 player position: 17
Now another state consisting of these data has to be stored:
State 2: box positions: 11, 13, 21, 33, 45, 47, 48, 49 player position: 10
State 2 can be stored relative to state 1 this way:
State 2: link to: state 1 boxNo: 0 newBoxPosition: 11 Player position: 10
Hash Function
Since the transposition table is usually implemented as hash table a hash function is needed for storing the states.
The hash function takes the position of every box and the normalized player position into account.
One efficient way to implement this is using Zobrist values (see: Albert L Zobrist. A new hashing method with application for game playing. ICCA journal, 13(2):69–73, 1970.)
Normalizing the player position
Solvers not interested in finding solutions optimized for moves can consider two states equivalent if the boxes are at the same positions and the player positions are in the same player access area.
This can be implemented by storing only normalized player positions, e.g. the top-left reachable position instead of the actual position of the player.
This significantly reduces the number of states in the search tree.
Calculation of player reachable positions
The reachable player positions must be calculated very often during the solver search. Hence, an efficient algorithm is required.
Algorithm
In order to generate successor states from a specific state during the search the solver must know which side of which boxes the player can reach.
Instead of calculating a path for the player to every side of every box separately it’s quicker to calculate all player reachable positions at once.
This can be done by performing a simple Breadth First Search.
The BFS marks all reachable positions. This can be done by using a boolean array where each bit represents a specific position on the board.
For a better performance time stamps can be used to mark the reachable positions of the player instead of boolean flags.
Brute force
The first step we do is to code a routine that generates all possible pushes for a given level situation. In our level for the first push there are four possible pushes: up, down, left and right. All of these pushes are done and the resulting states are stored in a queue.
With only one push the box can be pushed to the following positions:
After this is done we take every of these saved states as new start state and generate all possible successor states. For example, this is one state than occurs after the first push has been made:
We take this state and generate all successor states of it (that just means we push the box to every possible direction again). Again we save every generate state in the queue.
Described as algorithm this looks like this:
This is done again and again:
- Add the initial state (the level begin) to the queue
- Take the first state of the queue
- Generating all successor states of the state we got of the queue
- Add all states we've just generated in the queue
- continue by step 1
Finally we reach the state where the box is located on the goal.
Pruning duplicate positions
The described algorithm can be improved a lot. One thing that can be improved is the following: At any time the algorithm pushes the box on square to the right. Then it adds this state to the queue. At some time it takes this state from the queue again and generates all successor states - including the state resulting by pushing the box one square to the left. This results in a loop: Pushing a box to the right, then back to the left, again to the right, ... we generate duplicate positions which slows down the search a lot. So what we have to do is avoiding duplicates states. To avoid duplicate positions we have to detect them. Therefore we have to store every state reached during the solving process. After a new state has been generated we have to check if it has already been generated before and if so we just discard it. This reduces the number of states to search until a solution is found a lot and therefore improves the performance of the solver.
New solver process logic:
- Take the first state of the queue
- Generating all successor states of the state we got of the queue
- Delete all successor states that have already been generated before
- Add all left states to the queue
- continue by step 1
Deadlocks
Due to the constraints given by the rules of Sokoban some states in the game are deadlocked.
That means it isn’t possible to push every box to goal, anymore.
In general, deadlocks can be arbitrarily complex and potentially include all the boxes.
Hence, detecting all deadlocks is only feasible for very small levels.
However, a lot of deadlocks can be identified also in bigger levels.
Detecting deadlocks can prune huge parts of the search tree and therefore is an important part of every solver.
A balance has to be found between the time spent on deadlock detection and the time spent on the actual search.
While the detection process itself has some computational cost, the benefits of pruning large parts of the search tree usually outweigh the drawbacks.
See the Deadlocks section for an overview of some common deadlocks that may occur.
Pushes Lowerbound Calculation
The ability to admissibly estimate the number of box pushes needed to solve a specific state is useful for the heuristic function used in a guided search - like for example the A*-search.
The more accurate the calculated lower bound is the better it can guide the search.
However, calculating a good lower bound is a CPU intensive calculation.
A good lower bound calculation is especially important for solvers that search push optimal solutions.
The lower bound can also be used as information whether a level has been solved, since a lower bound of 0 means all boxes are on goals.
Performance vs. Accuracy
Calculating an accurate pushes lower bound is a quite expensive task.
Hence, depending on the needed accuracy different algorithms are used.
Free Goals Count
A trivial lower bound can be calculated by counting the number of goals not occupied by a box.
This calculation is very fast but the results are quite inaccurate.
However, this calculation can be used to identify specific level types.
Example:
If the initial state of a level has 20 boxes but only one goal not occupied by a box then this level belongs to a specific level type where most of the boxes are on goals right from the beginning.
For such levels a lower bound calculation can often not guide the search as well as in other level types.
Simple Lower Bound
A simple lower bound calculation calculates the sum of the distances of each box to its nearest goal.
The distance from a box to its nearest goal can be calculated with various degrees of sophistication.
The simplest method is to calculate the so-called Manhattan distance.
A more accurate method is to use the minimum push distance from a box to its nearest goal.
The program can precalculate the minimum push distance to the nearest goal for all squares on the board during initialization.
That way, it's a simple and efficient table lookup to find the distance to the nearest goal for each box during the search.
Both of these methods have the notable property that they are so-called admissible heuristics, i.e., they never overestimate the true shortest solution. This means the lower bound estimate can be used for solving a level with a push-optimality guarantee.
Calculating a simple lower bound is fast and accurate enough for very small levels. It does, however, grossly underestimate the true lower bound in most cases. The simple lower bound ignores that all boxes must go to different goals, and it also ignores how the boxes interact with (typically block) one another.
Minimum Matching Lower Bound
The Minimum Matching Lower Bound algorithm calculates a minimum-cost perfect matching on a bipartite graph.
The “cost” is represented by the push distance of a specific box to a specific goal.
Each box is assigned to a goal so that the total sum of distances is minimized.
The matching can be calculated using the Hungarian method or the Auction algorithm, for instance.
The complexity of this calculation is about O(N3), where N is the number of boxes and therefore are quite expensive calculation.
The benefits of this expensive calculation are:
- It produces much more accurate results than the Simple Lower Bound calculation.
- It provides the parity of the any solution, i.e. if the value returned by the algorithm is even, then the number of pushes in a solution is also even.
This makes it possible to skip every other iteration in an iterative deepening search.
- It can detect deadlocks where not every box can reach an own goal anymore.
Greedy approach
Calculating a minimum-cost perfect matching on a bipartite graph as described above is an expensive computation.
A greedy approach can be used to approximate a minimal perfect matching:
the push distances of all boxes to every goal are calculated and stored in a list sorted ascending by distance.
Example:
- box1 to goal 1: distance = 3
- box 2 to goal 1: distance = 4
- box1 to goal 2: distance = 10
- box 2 to goal 2: distance = 12
There is also a list of all already matched boxes and goals.
We then iterate over this list of distances.
If the box and the goal both aren’t matched, yet, we match them.
In the example, we would match box 1 to goal 1.
Then the second list entry is reached:
“box 2 to goal 1: distance = 4“
Since goal1 is already matched with box 1 the box can’t be matched and we discard this entry.
However, it is possible that not every box is assigned a goal after the list has been completely iterated over – although a valid matching for all boxes may be possible.
In that case all not yet matched boxes are simply assigned to its closest goal.
This approach isn’t as expensive to calculate as a minimum-cost perfect matching with the disadvantage of being less accurate.
Algorithm Optimization
The algorithm used to calculate the pushes lower bound can be optimized using specific optimization ideas:
- If the lower bound of a state is L1 and a push is made the new lower bound L2 has to be calculated.
When the algorithm finds a matching that reduces this lower bound L1 by the cost of the push, it’s clear that the lower bound can’t be reduced further.
Hence, the algorithm can stop immediately in these cases.
- During the search the algorithm only needs to update the previous found matching, because each push results in only one box changing its distances to the goals.
- Only perfect matchings are relevant.
Hence, as soon as it is clear that a perfect matching isn’t possible the algorithm needn’t to search for the minimum matching anymore.
Calculating the Box Distances
For calculating the pushes lower bound the algorithm needs the distances for all boxes to all goals.
Calculating these distances can be done in different ways.
Since the wall positions and goal positions never change, the distances for a specific box depend on:
- the player position
- the positions of the other boxes
Calculating the real distances for all boxes regarding all other box positions is too difficult and time consuming. In fact this can be as difficult as the task to solve the whole level.
Hence, the common practice is to just consider the distance of a box to a goal under the assumption that no other box is on the board.
This also has the advantage that the distances can be computed and cached before the solver starts since they never change while the solver is running.
Position of the Player
For a more accurate calculation of the distance of the box to the goals the player position can be taken into account.
The needed pushes to push the box to the goal having the player on the right of the box is 6 pushes.
However, the needed pushes to push the box to the goal having the player on the left of the box is only 2 pushes.
Hence, it's necessary to calculate the distance of the box to the goals for every possible player access area.
In this example there are two possible player access areas: one having the player left from the box and one having the player right from the box.
The player position has also to be taken into account of for calculating the real distance of the box to the goals.
There is only one player access area in this example.
However, the box distance to the goal is not 2 pushes but 8 pushes.
Both examples have something in common:
There is a so called Gate Square.
- Gate Square
- A Gate Square divides the board into at least two different player access areas.
If the goal distances of a box on a Gate Square has to be calculated the player position has to be taken into account (like in Example 1).
Gate Squares in general have to be taken account of when calculating the box distances, like shown in Example 2.
This is example 2 with the Gate Squares highlighted:

Linear Conflicts
The restriction of only considering one single box for calculating the box distances has the obvious disadvantage of not taking into account other boxes that may block the box or the player.
It's however possible to detect some of the box configurations that inevitably increase the calculated pushes lower bound.
In this example the calculated pushes lower bound is 8 pushes when using the Minimum Matching Lower Bound calculation.
However, the real number of needed pushes to push both boxes to a goal is 10 pushes.
The reason for this is both boxes block each other in a way that both boxes can only be pushed vertically. Since all possible vertical pushes will push a box further away from a goal the needed pushes for solving the level increases.
In such situations the calculated pushes lower bound can be increased by 2.
Pitfalls
This example shows three boxes that all can only be pushed vertically.
However, this doesn't mean that we can add a penalty higher that 2 to the calculated pushes lower bound.
Since pushing the middle box down (or up) makes it possible to push the other two boxes push optimal to the goals only a penalty value of 2 may be added to the calculated pushes lower bound.
Note: if there were a wall above or below the middle box it would be valid to add a penalty value of 4!
This example is the same as Example 1 but with one goal at a different position.
Since now a vertical push of the middle box is on the push optimal path to a goal it's not valid to add any penalty value to the pushes lower bound!
Complex linear conflicts
Sophisticated conflict detection algoritms may also detect linear conflicts involving more than two boxes and more complex linear conflics like in this example:

Frozen Boxes
The distanes used for the lower bound calculation are usually precomputed before the solver search starts.
They represent the number of box pushes required to push a box from any square on the board to any other square.
These distances are optimistic distances in that they assume no interference with other boxes.
The only restrictions are the walls on the board.
However, boxes on a goal which can't be pushed anymore (-> frozen box) can be treated as walls. They therefore potentially change the distances.
In this example the pushes lower bound is 3 pushes.
However, when the left box is pushed two squares to the right to its goal the right box can't be pushed up immediately anymore:

In such situations the box distances have to be recalculated while treating the box on the goal as a wall.
By doing so the correct pushes lower bound can be calculated.
Pattern databases
Some solver programs use pattern databases where precalculated box configurations are stored together with a penalty value.
This way it's possible to detect even complex penalty situations and add high penalty values.
No influence pushes
Tunnels
Having teached the solver to use the algorithms described above our little level is solved very quickly. Usually Sokoban levels are a lot more complicated. Therefore we have to search for further ideas how to reduce the number of states we have to generate during the solving process.
New example level:
Here we have a (still very easy) level containing two boxes. The solver takes the given state as initial state. Then it generates all possible successor states. This means: Pushing box 1 to every possible direction AND pushing box 2 to every possible direction. The solver doesn't know which push is the best for solving the level - hence it has to generate all possible successor states. This soon leads to an enormous number of generated states (at least in larger Sokoban levels). It would be a great advantage if we knew that only pushes of one box are relevant in a specific state.
Let's assume the player has just pushed the box next to him one square to the right. What to do next?
The solver will consider every possible next push: all possible pushes of the higher box and all possible pushes of the lower box. But: The higher box is in a tunnel - the just performed push has been a "no influence push". The reason is: The squares the lower box can ever be pushed to stayed the same. There aren't any additional squares the lower box can reach, nor are there any squares the lower box can't reach due to the push of the higher box. The just pushed box has definitely to be pushed sooner or later. So there is no reason why not to push it further to the right immediately!
In general such a "no influence push" is always created when the situation AFTER the push looks like this (or any flipped / mirrored version of it):
Every time a push of a box results in such a situation the box can immediately be pushed one square further! This rule can reduce the number of states to be generated in some levels a lot.
PI-Corrals
This section describes an admissible domain-dependent move pruning technique for the Sokoban game called PI-Corral pruning.
PI-Corral pruning has highly attractive properties for a Sokoban solver program:
- It prunes a significant number of states from the search
- It steers the search towards positions with a certain class of deadlocks, thereby helping to detect these deadlocks early on, increasing the pruning even further
- It preservers push-optimality guarantees provided by the solver
PI-Corral pruning leverages the same idea that is also used for pruning due to tunnels: It identifies pushes that don’t influence certain parts of the board and then ignores all boxes that aren’t influenced by the performed push.
A simple example of a PI-Corral:

In this level the player just has pushed the box to the left.
Normally the solver now generates all possible pushes for all boxes including the box in the lower right corner. The push creates an area the player can't reach marked with a ![]() .
.
The boxes that are part of this area can only be pushed inside this corral (= on squares that are marked) with the next push. Hence, these pushes don’t have any impact on the rest of the level. The reachable player positions aren’t reduced and also the reachable positions of the box in the lower right part of the board aren’t reduced.
At least one of boxes at the border of the marked area must be pushed into that area sooner or later. This is always necessary when a box at the border or inside the area isn't located at a goal square, or when a goal square inside the area isn't filled with a box. In the current position, the player can make all the possible pushes which ever can be made into the marked area. Therefore, the solver just needs to generate the pushes for the boxes at the border of the marked area. The legal pushes for all other boxes on the board can be ignored.
This can reduce the pushes to be generated a lot - particularly when there are a lot of boxes in the level that aren't involved in the PI-Corral.
The key insight with PI-corrals is the fact that as the boxes on its barrier can only be pushed inwards, one of them will indeed have to be pushed there before any of the boxes in the corral can be pushed elsewhere.
So, if the corral has to be dealt with eventually, it is best to deal with it right away and all pushes of other boxes can be discarded.
The reason that this works, and that it only applies to PI-corrals and not other corral types is due to box influence.
In a PI-corral no other box can be influenced by the fact that a box is pushed into the corral, because any boxes outside the PI-corral are by definition either accessible or inaccessible regardless of whether the player can walk in the area of the corral, while boxes completely inside the corral (not on the boundary) are by definition inaccessible to the player and could not be pushed before the corral is dealt with.
In other words: all the pushes of boxes not part of the PI-Corral are still possible after a box is pushed into the PI-Corral.
Terms and Definitions
- Corral
- The boxes and walls on the board can split the board into several areas.
- An area of the board which the player cannot reach, surrounded by a barrier made of one or more boxes, and any number of walls is called “corral”.
- The corral includes all the boxes on the barrier between the inside and the outside of the corral, and all interior boxes, if any.
- An example corral:
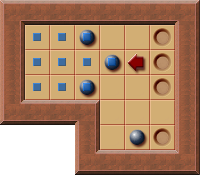
- Positions part of the corral are marked with
 .
.
- I-Corral
- A corral where all boxes on the barrier can only be pushed inwards (into the corral) by the first push.
- The "I" in "I-corral" is a reference to "inside" or "inward".
- An example corral:
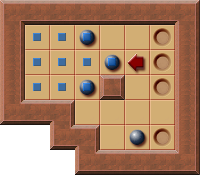
- Positions part of the I-corral are marked with
 .
.
- Note how in this I-Corral example (in contrast to the Corral example) it's not possible to push any box to a position not part of the corral.
- PI-Corral
- An I-Corral where the player can perform all legal first pushes into the corral,
- meaning the player can reach all the relevant boxes from all relevant directions.
- The "P" in "PI-Corral" is a reference to "player" or "pusher".
- A "PI-Corral" is the important sub-class of the I-Corrals where the player can reach all the boxes on the barrier of the corral and perform all their legal inwards pushes.
- An example PI-Corral:
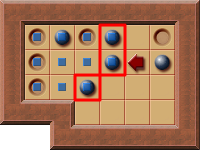
- The boxes on the barrier of the PI-Corral are highlighted in red.
-
- Counter-example: an I-Corral which isn't a PI-Corral because of the outside blocking box:
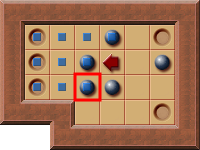
- This example isn't a PI-Corral because the player cannot push the highlighed box inwards;
- there is an outside box that blocks the access.
- Note that if that outer box was a wall then the level is a PI-Corral:
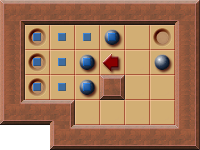
- The rule is: the player must be able to perform all legal inwards pushes of the PI-Corral boxes on the barrier.
- This can be checked: remove all boxes which aren’t part of the PI-Corral, then compare the possible pushes.
PI-Corral Pruning
The PI-Corral property in itself is not enough to permit pruning states from the search.
There is the additional constraint that sooner or later, at least one of the boxes on the barrier must be pushed into the corral in order to solve the puzzle.
There are different reasons why such a push may be necessary, so this constraint can be implemented with various degrees of sophistication.
The constraint "Pruning is only permitted if at least one box in the PI-Corral is not on a goal square, or if at least one goal square in the PI-Corral does not contain a box" can be implemented by simple inspection of the board position.
A more sophisticated solver may form plans which permit pruning for more involved reasons, e.g., "The player must pass though the corral", or "A box from the outside must be parked inside the corral".
If there is a PI-Corral and one of the involved boxes has to be pushed in any way to solve the level then PI-Corral pruning can be applied. That means in such a situation the solver only has to generate pushes for boxes part of the PI-Corral but not for boxes outside the PI-Corral.
The key-insight is this: pushing a box inwards, into the PI-Corral, never affects the player's access to boxes outside the PI-Corral. Therefore, when we choose which box to push next, we might as well push one of the PI-Corral-boxes because we have to do that sooner or later anyway.
In the next push, we still have full access to all boxes outside the corral so we can pick one of them, if we wish to. However, if there still is a PI-corral on the board, we continue only checking if PI-Corral pruning can be used and if yes, we again only consider the PI-Corral-boxes for generating new board positions.
So the bottom line is that for each position we meet during the solving process, we first check for PI-corral pruning, and if it can be applied, we never generate pushes for boxes outside the PI-corral.
A very simple example of a PI-Corral is a tunnel:
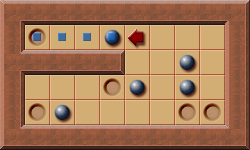
In this simple PI-Corral all conditions are fulfilled:
- there is a corral
- all possible pushes of the boxes on the corral barrier are pushes into the corral
- at least one of the boxes in the corral has to be pushed to solve the level
- the player can perform already now all theoretically possible legal pushes (not generating a deadlock) into the corral
Hence PI-Corral pruning can be applied and only pushes of the marked box must be considered for the next push.
In this simple example the key idea behind PI-Corral pruning becomes clear:
There may be some complicated push sequences needed to push the boxes outside the PI-Corral to goals. However, no matter how complex these push sequences may be: all of these pushes are still possible after the box has been pushed into the PI-Corral.
The push of the box into the PI-Corral has no "influence" on the rest of the level.
Multi Room PI-Corral
It's rather seldom that a board position contains simple PI-Corrals like the one depicted above.
Even when there is an I-Corral, the player seldom has access to all the boxes (from all the required directions).
Often, the player's access to the I-Corral boxes is blocked by neighboring corrals like in this (small) example:
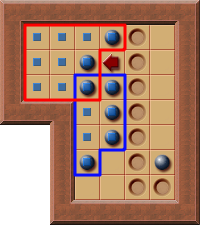
Neither does the top-left corral (red border) nor the neighboring corral (blue border) fulfill all PI-Corral constraints.
In both cases there is a box which can't be pushed into the corral at the moment (the box having a red and a blue border).
However, both corrals can be combined to a multi room corral.
The combined corral then fulfills all PI-Corral constraints:
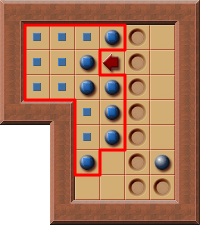
In order to find these Multi Room PI-Corrals the algorithm combines corral after corral until a (multi room) PI-Corral has been found.
This way the algorithm also ensures that there are as few boxes in the found PI-Corral as possible.
The marked area is a (combined) PI-Corral, since the boxes can only be pushed into the corral and all of the legal pushes are currently possible.
However, when the algorithm starts with the top-left I-Corral, this corral is classified being a PI-Corral without the need to combine it with another corral:
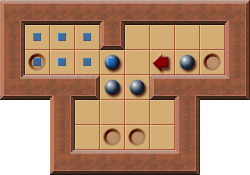
This means instead of two boxes there is only one single box to consider for the next push.
Note:
After having pushed the PI-Corral box one square into the PI-Corral there are two PI-Corrals now:
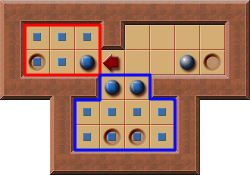
In such a situation the solver can choose which PI-Corral to consider first.
This is another example showing the importance of the algorithm only combining corrals if necessary:
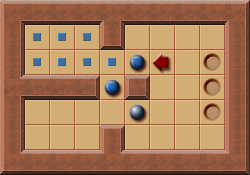
This example also shows that a deadlock detection can help identifying PI-Corrals.
The marked PI-Corral has two boxes.
However, only one of the boxes can currently be pushed into the PI-Corral.
Nevertheless it's a PI-Corral because pushing the lower left box of the PI-Corral into the PI-Corral creates a deadlock and therefore this isn't a legal/valid push.
Deadlock Situations
PI-Corral pruning can help detecting deadlocks earlier as a side-effect of successor-pruning.
If there is a (smallish) deadlock situation on the board consisting of a PI-Corral, then pruning leads to a position where the legal moves dry out, in effect finding a deadlock like in this (very small) example:

The solver only considers these boxes for the next push. Since no further legal push is possible (assumed that “freeze deadlocks" can be detected by the solver) a deadlock is detected.
Statistics
In his solver scribbles Brian Damgaard wrote:
There is always an overlap when different pruning techniques are used in a solver, but conservatively speaking, this new technique [PI-Corral pruning] is itself able to prune at least 20% of the search tree according to my experiments, and empirically the savings always outweighs the extra costs.
My program uses precalculated deadlocks to handle simple deadlocks like this one, but the corral-pruning is a valuable contribution to the program, and experiments shows that the corral-pruning almost can hold its candle to the precalculated deadlocks, if it is asked to do so:
Statistics - SokEvo/107 - Forwards search - no packingorder - AMD 2600+ Configuration A: A* search + transposition table Configuration B: A* search + transposition table + corrals Configuration C: A* search + transposition table + precalculated deadlocks Configuration D: A* search + transposition table + precalculated deadlocks + corrals
"B" is the experiment with corrals only, without precalculated deadlocks, and its 21 seconds (on my amd 2600+ pc) is in the same league as the "C" experiment with precalculated deadlocks but no corral-pruning. "D" with all currently implemented pruning techniques reduces the total solving time to 7 seconds, showing that the different pruning techniques work well together.
| Solver Statistics | |||
|---|---|---|---|
| Configuration | Generated states | Pushes | Time |
| A | 11974023 | 51938064 | 65 seconds |
| B | 4632203 | 11918161 | 21 seconds |
| C | 2030736 | 7011203 | 11 seconds |
| D | 1231376 | 3299797 | 7 seconds |
Temporary Auxiliary Pushes
Usually there are a lot of I-Corrals for which the player can’t perform all inwards pushes at the moment.
One box is blocking the player from pushing one of the boxes into the I-Corral.
An obvious aim now is to push this blocking box away to create a PI-Corral.
This destroys push optimally guarantees but results in more detected PI-Corrals and therefore in a smaller search tree for the solver.
One way to check whether the box can be pushed away is to check whether the box can be pushed away and then immediately back to where it is now. If this is possible, we can perform all pushes into the I-Corral and after that is done the blocking box is always back where it is now.
Currently this is not implemented in any solver.
A subclass of those “I-Corrals with access blocking boxes” could be used for pruning with some further investigations.
The marked box of the I-Corral can’t be reached by the player.
However, through further calculations the program could prove that the I-Corral can never be opened by pushing this box.
Pushing the box into the corral does never allow the player to push any other corral boxes.
Hence, in these seldom situations even pruning on I-Corrals may be applied.
This also preserves push optimality.
"Real world" PI-Corral Examples
The program JSoko. offers a debug mode for testing PI-Corral pruning.
The shown example PI-Corrals are taken from JSoko version 1.81 having that debug setting activated.
To let JSoko highlight the found PI-Corrals:
- Start JSoko
- Type the letters “debug” when JSoko has the keyboard focus. This shows a new menu called “debug”
- In the debug menu select “Show I-Corral during solving"
Note: although the menu text is "Show I-Corral" JSoko will show PI-Corrals and only those for which PI-Corral pruning can be applied.
Note 2: PI-Corrals that include all boxes on the board aren’t shown by JSoko since there is no benefit in applying pruning when all boxes are part of the PI-Corral.
When the PI-Corral debug settings is activated JSoko will check for PI-Corrals and highlight them after every push that is made.
Thinking Rabbit - Original Level 1:
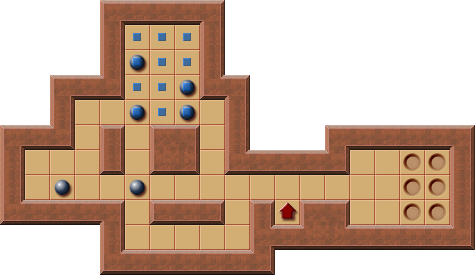
Due to PI-Corral pruning the solver has only to consider the PI-Corral boxes for the next push, only one of which is currently reachable for the player.
This example shows that a deadlock detection can help detecting PI-Corrals.
The lower left box of the PI-Corral isn't reachable by the player at the moment.
However, both pushes of that box would result in a freeze deadlock.
Hence, no legal push is possible for this box.
Thinking Rabbit - Original Level 3:
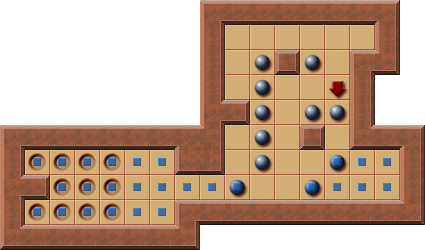
In the shown situation the solver has choose which PI-Corral to consider first.
Thinking Rabbit - Original Level 4:
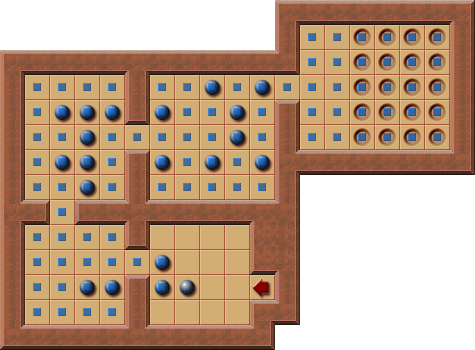
There is a huge multi room PI-Corral containing nearly all of the boxes.
Nevertheless, PI-Corral pruning can also help pruning some states for the solver in such situations where only one box is outside the PI-Corral.
Thinking Rabbit - Original Level 6:
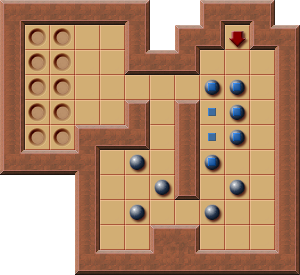
This is an example where a sophisticated deadlock detection can help to detect more PI-Corrals.
Thinking Rabbit - Original Level 10:
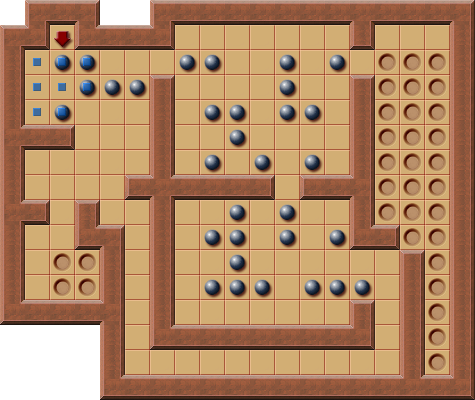
This example shows that JSoko detects some PI-Corrals where pruning is possible but not that useful.
Since there is only possible push there is nothing to be pruned.
Thinking Rabbit - Original Level 15:

The player is surrounded by a huge multi room PI-Corral.
Every push of one of the PI-Corral boxes results in a further PI-Corral that can be used for pruning.
Figure 3 level of an article about PI-Corral pruning:
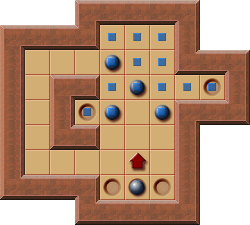
There is an article about PI-Corrals written by Renato R. Leme, André G. Pereira, Marcus Ritt and Luciana S. Buriol where the authors claim that JSoko and YASS can't detect the correct PI-Corral in the shown level.
However, the screenshot shows that JSoko can correctly identify all the boxes and positions that are part of the PI-Corral (and so does YASS)!
Note: an additional box has been added to this example level (the box on the goal below the player) because JSoko only highlights PI-Corrals that don't contain all boxes. However, this extra box doesn't affect the PI-Corral detection used in JSoko (and YASS).
Parking
Many levels cannot be solved by just pushing one box at a time to the goal position.
Most levels are constructed in such a way that some of the boxes have to be specifically rearranged to make room for pushing other boxes.
In some cases boxes have to be actually pushed over a goal position to a “parking” position, from where they can then later be pushed to their final goal position.
YASS Solver
Sokoban solver "scribbles" by Brian Damgaard about the YASS solver
Sokolution Solver
Sokoban solver "scribbles" by Florent Diedler about the Sokolution solver
Solver "Rolling Stone"
Limited search
Ideas by David Holland on computer solving by limited search are linked below. They aren't fully wikified yet as author has RSI. Features new concepts such as free space, shuffling, relocation and generalized deadlock detection. Sketches of algorithms included. Other new concepts such as goal traps with algorithms may be implemented in existing solvers. Author hopes other programmers will discuss and implement what they find relevant. Limited search as opposed to exhaustive search uses macros, heuristics and domain-specific knowledge to effectively search deeper in the tree of positions by not looking at every position. A new category of "Planner" plug-in is suggested for limited search to be tried when the Solver plug-in fails, indicating too large a tree. David Holland's computer Sokoban solving ideas