Solver

From Sokoban Wiki

(Difference between revisions)

Briandamgaard (Talk | contribs)
(→YASS Solver)
Newer edit →

Revision as of 08:38, 1 February 2010

Let's program a little solver for Sokoban.

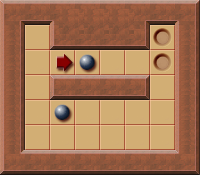
The level to solve looks like this:

Brute force

The first step we do is to code a routine that generates all possible pushes for a given level situation. In our level for the first push there are four possible pushes: up, down, left and right. All of these pushes are done and the resulting states are stored in a queue.

With only one push the box can be pushed to the following positions:

After this is done we take every of these saved states as new start state and generate all possible successor states. For example, this is one state than occurs after the first push has been made:

We take this state and generate all successor states of it (that just means we push the box to every possible direction again). Again we save every generate state in the queue.

Described as algorithm this looks like this:

This is done again and again:

Add the initial state (the level begin) to the queue

Take the first state of the queue
Generating all successor states of the state we got of the queue
Add all states we've just generated in the queue
continue by step 1

Finally we reach the state where the box is located on the goal.

Pruning duplicate positions

The described algorithm can be improved a lot. One thing that can be improved is the following: At any time the algorithm pushes the box on square to the right. Then it adds this state to the queue. At some time it takes this state from the queue again and generates all successor states - including the state resulting by pushing the box one square to the left. This results in a loop: Pushing a box to the right, then back to the left, again to the right, ... we generate duplicate positions which slows down the search a lot. So what we have to do is avoiding duplicates states. To avoid duplicate positions we have to detect them. Therefore we have to store every state reached during the solving process. After a new state has been generated we have to check if it has already been generated before and if so we just discard it. This reduces the number of states to search until a solution is found a lot and therefore improves the performance of the solver.

New solver process logic:

Take the first state of the queue
Generating all successor states of the state we got of the queue
Delete all successor states that have already been generated before
Add all left states to the queue
continue by step 1

inside View to "Pruning duplicate positions"

Detecting deadlocks

During the search the solver will generate states that are deadlocks. That means the level can't be solved from this point on, no matter how we push the box. See the Deadlocks section for an overview of some common deadlocks that may occur. To avoid deadlock states and thus reducing the number of states to be searched we now have a new process logic:

Add the initial state (the level begin) to the queue

Take the first state of the queue
Generating all successor states of the state we got of the queue
Delete all successor states that have already been generated before
Delete all successor states that are deadlock
Add all left states to the queue
continue by step 1

How to detect deadlocks

Lowerbound

Having a look at our test level we (as humans) just "see" that only pushes to the right are pushes that let us come closer to a solution. A push to the left is useless. What do we "see" here ? Well, we see, that the goal is on the right side. If we want to get to something that is right to us we won't go to the left :-) So let us teach the solver to be intelligent enough to recognize which direction it should prefer. Therefore we calculate for every square how many squares it is away from the goal:

Every time the solver generates a new state it takes the number stored at the square the box is located after the push. For instance: At the start of the level (initial state) the player may push the box on square to the left. The new state is saved in the queue - and, the number of the square the box now is located at is stored in the queue (in this example it would be "4"). The number represents the distance of a specific square to the goal and is saved together with a state in the queue.

The next time the solver takes a state from the queue it takes the state having the lowest stored distance!

Here it is in detail. Let's assume every square in the level has a coordinate. The player is located at position: 3, 4 for example and the goal is located at 7, 4.

The solver takes the initial state out of the queue and generates all successors. It also saves the distance together with every state. From the initial state the solver generates these four successor states (the order is arbitrarily):

State	box position	distance to goal
1.	4,3	4
2.	3,4	4
3.	4,5	4
4.	5,4	2

The solver now won't take the first state of the queue but the one having the lowest distance to the goal, this is state number 4.

This way it prefers the path to the right and generates fewer states until it finds a solution for this level. It takes state 4 from the queue and generates its successor states. Again the distances are stored together with the successor states in the queue. And again the state with the lowest distance is take from the queue next. This way we reduce the number of generated sates during the solving process.

To ensure that the solution we found is the solution with the fewest possible pushes, the distance should also consider the distance from the start state. For example, the distance could be the estimated solution length. It is calculated as distance_from_start + underestimated_distance_to_goal. The underestimation ensures that no shorter solution will be missed.

Advanced lowerbound calculation

No influence pushes (tunnels)

Having teached the solver to use the algorithms described above our little level is solved very quickly. Usually Sokoban levels are a lot more complicated. Therefore we have to search for further ideas how to reduce the number of states we have to generate during the solving process.

New example level:

Here we have a (still very easy) level containing two boxes. The solver takes the given state as initial state. Then it generates all possible successor states. This means: Pushing box 1 to every possible direction AND pushing box 2 to every possible direction. The solver doesn't know which push is the best for solving the level - hence it has to generate all possible successor states. This soon leads to a enormous number of generated states (at least in larger Sokoban levels). It would be a great advantage if we knew that only pushes of one box are relevant in a specific state. Let's assume the player has just pushed the box next to him one square to the right. What to do next ? The solver will consider every possible next push: all possible pushes of the higher box and all possible pushes of the lower box. But: The higher box is in a tunnel - the just done push has been a "no influence push". The reason is: The squares the lower box can ever be pushed to stayed the same. There aren't any squares the box can reach more nor are the any squares the lower box can't reach due to the push of the higher box. The just pushed box has definitely to be pushed sooner or later. So there is no reason why not to push it further to the right immediately!

In general such a "no influence push" is always be created when the situation AFTER the push looks like this (or any flipped / mirrored version of it):

or

Every time a push of a box results in such a situation the box can immediately be pushed one square further! This can reduce the number of states to be generated in some levels a lot.

Advanced tunnel detection

ICorrals

Tunnels can reduce the number of boxes to consider for the next push to only one. Thus, the solver is generating either all possible pushes of all boxes (normal case) or just the possible pushes of just a specific box (box in a "tunnel"). Is there any thing in between ? Yes, it is.

In this level the player just has pushed the box to the left. Normally the solver now generates all possible pushes for all boxes including the box in the lower right corner. The push created the corral (area the player can't reach) marked with a . The boxes involved in this corral can only be pushed inside this corral (= on squares that are marked). All pushes of these two boxes don't influence the other box. One of the pushes that lead to the inside of the corral has to be done sooner or later - and there is no reason why it can't be done immediately!